Interface編集部

FPGA設計は論理回路図よりも真理値表が便利
~シャノン展開式はルックアップ・テーブルと相性抜群~
FPGAは任意の機能を実現するために真理値表が使われ,それをルックアップ・テーブル(LUT:Look-Up Table)のかたちで実装する方法が使われています.そこで今回はFPGA(Field Programmable Gate Array)の中でもプログラム可能な論理(PL:Programmable Logic)部分の仕組みついて解説します.具体的には,このPLの中に配置可能なCLB(Configurable Logic Block)という論理ブロックがあり,これを支える仕組みに関する内容です.
真理値表とルックアップ・テーブルで論理回路を実装できる
●設計対象が複雑な場合は論理回路図では見づらくなる
論理回路はAND(論理積),OR(論理和),NOT(論理否定),XOR(排他的論理和)などの記号を回路図で表します.これらはウィキペディアによると「MIL論理記号」と呼びます.MILはMilitaryから来ていて,米国の軍事規格に由来しています.
設計する回路が簡単な頃は,視覚的に訴えるのに好都合だったかもしれませんが,現在では複雑な回路網を扱うようになったために,かえって煩雑になっています.そこで,設計する回路を論理回路図ではなく真理値表で表現することがよくあります.
●真理値表の良さ…セレクタ回路が真理値表そのものを直接デコードしてくれる
真理値表はすべての可能な論理を0と1の2値(ブール)関数で表現することができます.そして都合がよいことに,セレクタ回路が真理値表の関数値部分を入力すると真理値表そのものを直接デコードしてくれます.この理論的な背景については,本稿で詳しく解説します.要するに,真理値表表現を使えば,従来の論理回路図表現なしに任意の機能の論理回路がルックアップ・テーブルによってうまく実装できることが分かります.
▲カウンタ機能を真理値表で表現してみる
例えば,ある桁の1の数をカウントするとします.カウントすると上位桁に桁上げする出力(carry)とその桁の合計(sum)が出力されます.例えば3入力の1の数をカウントする場合を真理値表で表現すれば表1となります.
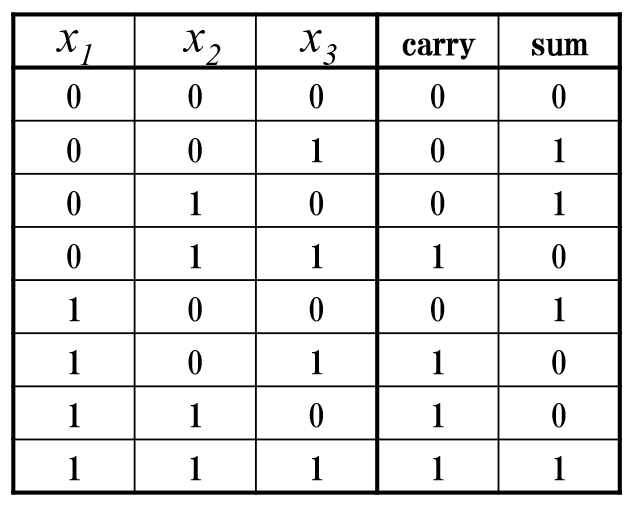
表1 3入力カウンタの真理値表
その桁の合計出力の真理値表をセレクタ回路で直接デコードする様子を図1に示します.
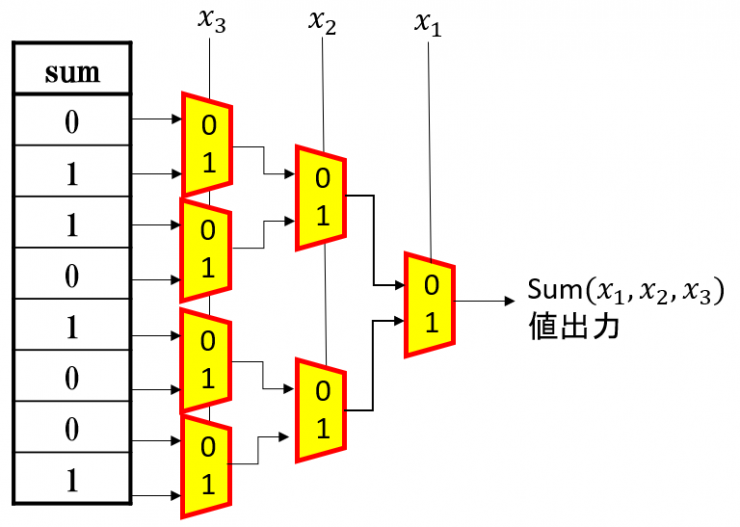
図1 3入力x1,x2,x3の桁の合計値をセレクタ回路でデコード
この後でセレクタ回路の定義と意味を解説するので,真理値表を見ながら入力から出力までの経路を追跡してみてください.また,桁上げ出力は合計の真理値表関数値と入れ替えれば出力できます.ただ入れ替えるだけで出力できる理由は.真理値表そのものは枠として変わらず,変わっているのは真理値表の関数値のみだからです.真理値表の枠が固定されているということは,それをデコードする回路,例えばセレクタ回路を設計するだけでよいわけです.
●ルックアップ・テーブルの役割
ルックアップ・テーブルとは,図2に示すように真理値表の関数値を構成メモリに格納し,それを内部入力として論理関数の種類をデコードする回路のことです.
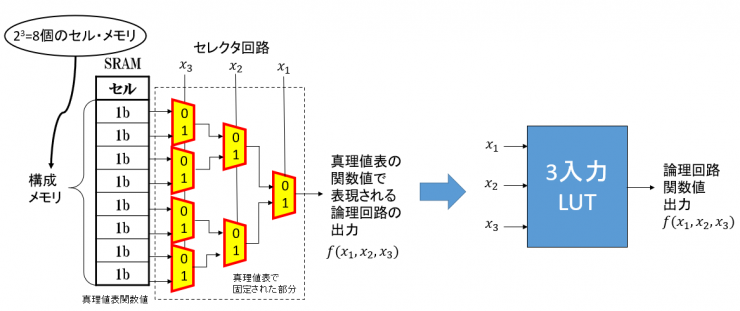
図2 3入力のルックアップ・テーブルの内部構造と回路表記記号
図2は3入力なので23=8個のセル・メモリで構成されています.また,構成メモリは,真理値表の関数値に対して,再設定可能なSRAMなどの1ビットのセルで構成されています.
ルックアップ・テーブルは,構成メモリに格納された内容によって,真理値表で表される1つの論理回路関数が選択され,その論理回路に外から入力される値により,その論理回路の出力が行われるという仕組みになっています(1,2,3)このように論理回路で表現しなくても真理値表を作成さえすれば,真理値表の関数値をルックアップ・テーブルに直接入力することで,真理値表が表す論理回路が実装できるのです.
セレクタ回路の働き
セレクタ回路の定義とその意味を解説します.fとgを入力してaが1のときはfを,aが0のときgを出力する回路をセレクタ回路と呼びます.論理式で書けば以下のようになります.
![]()
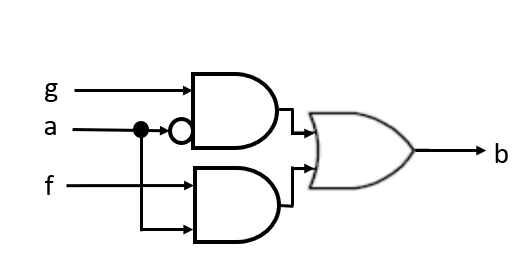
ここで,論理積記号は”・”で,論理和記号は”+”でそれぞれ表現します.論理積記号は省略することもあります.式(1)を論理回路で表すと図3(a)のように2段になります.
次に,セレクタ回路で表すと図3(b)のように1段で表せます.この理由は,現在のセレクタ回路はトランスミッションまたはパス・トランジスタと呼ばれるゲート回路によって実現されているからです.これはとても重要なことです.
 |
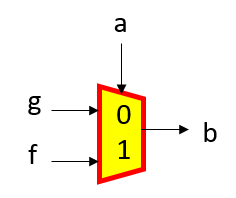 |
| 図3(a) 論理回路表記(2段) | 図3(b) セレクタ回路表記(1段) |
図3 セレクタ回路表記は論理回路表記よりも簡単
また,真理値表を書けば表2になります.
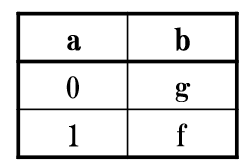
表2 式(1)の真理値表
シャノン展開からルックアップ・テーブルを作成しデコードまでの流れをみてみる
●入力が1つの場合…まずはシャノン展開をみてみよう
まず1入力のルックアップ・テーブルの例を使って解説します.1入力なので1変数関数f(x1)は,以下のように展開されます.
![]()
式(2)の展開の意味は,x1が0のとき,f(0)が選択され,x1が1のとき,f(1)が選択されます.それを回路図記号(セレクタ)で書いたのが図4です.
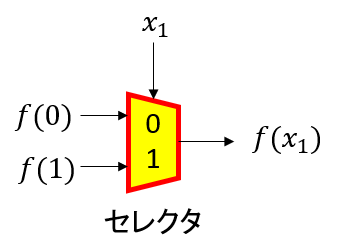
図4 式(2)を表現したセレクタ回路
真理値表にすれば,表3です.
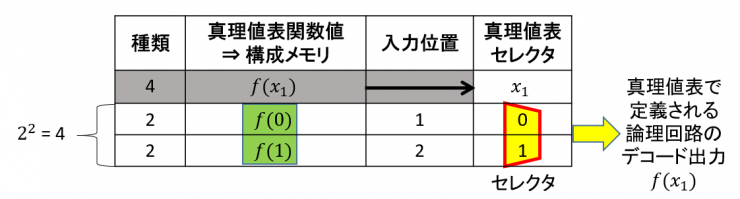
表3 式(2)を表現した真理値表
f(0)とf(1)は,それぞれ0と1の2通りの値をとることができるので,ブール関数の種類は2の2乗,つまり4種類です.たった1変数の例ですが,真理値表,真理値表関数値f(0), f(1),そして入力f(0)とf(1)がx1の0か1によって選択される,つまり,デコードされる様子が見事に表現されています.
ここで,式(2)の展開を「シャノン展開」と呼びます.そして,シャノン展開がこれからを解説するルックアップ・テーブルの仕組みにぴったりなのが,n変数の展開をせずとも直感的に分かります.これはすごいことで,筆者は執筆過程でこの事に気が付きました.
●入力が2つの場合…実際に式を展開してみよう
次に,2入力のルックアップ・テーブルの例を使って解説します.以下のような2入力関数f(x1, x2)を考えます.
![]()
この意味は,x1が0のときf(0, x2) を,x1が1のときf(1, x2) を選択します.次にf(0, x2) とf(1, x2) をx2について,それぞれ展開してみます.
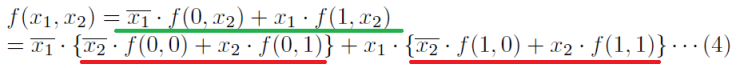
と展開されます.つまり,
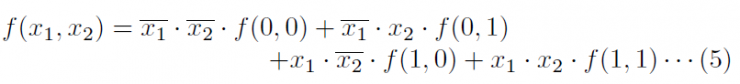
となります.これでシャノン展開について見通しがたちました.真理値表化してみると,表4になります.
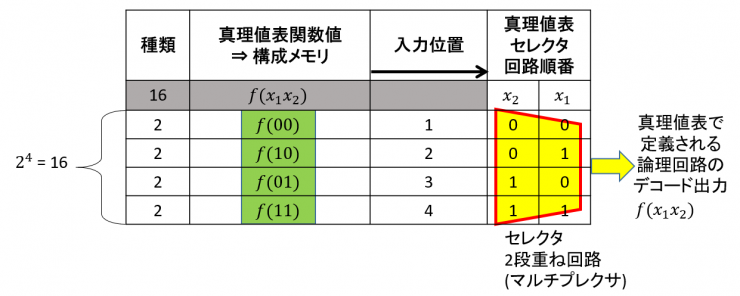
表4 式(5)を表現した真理値表
ここまででシャノン展開が真理値表表現になっていることがお分かりいただけると思います.デコードは,式(4)を括弧の内側から辿れば分かります.このように逆に辿るので,真理値表では変数が登場する順が逆になっていることに注意してください.2入力の場合は2の4乗,つまり16通りのブール関数があり,真理値表で表される論理回路と論理回路を組み合わせた回路図がどのような関係にあるかを表5に示します.
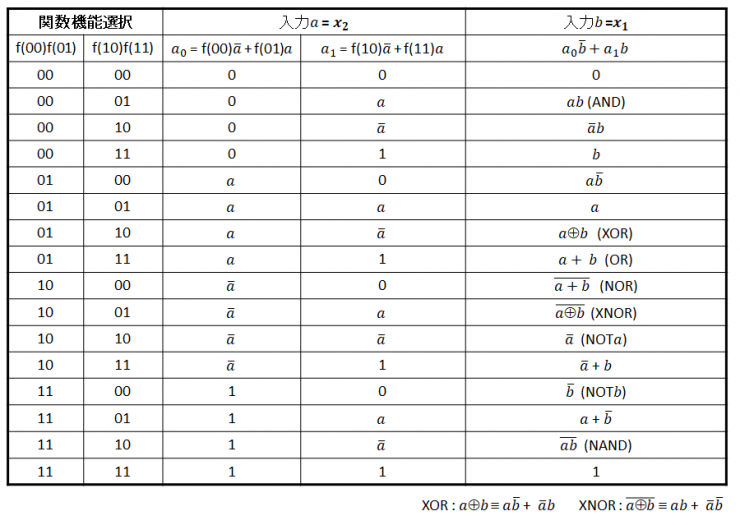
表5 ルックアップ・テーブルで実現される論理関数の選択表
構成メモリの設定によって,各関数機能が選択できます.2入力のルックアップ・テーブルによって回路が実現できていることが分かります.また,図5に2入力のルックアップ・テーブル・セレクタの2段構造と2段セレクタ構造を2重化したマルチプレクサ表記図を示します.
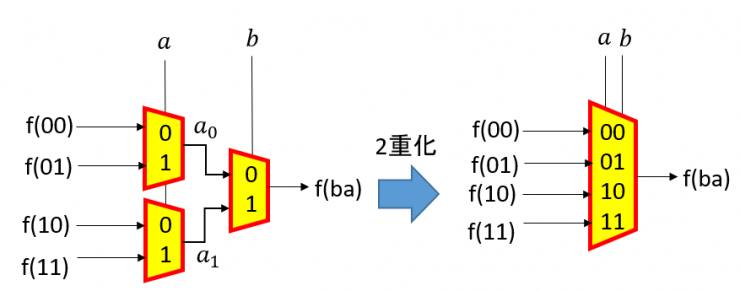
図5 2段のセレクタ回路を2重化したマルチプレクサ表記
●入力が3つの場合…ここまでくると式の展開規則がみえてくる
最後に3入力のルックアップ・テーブルの場合のシャノン展開を追っていきます.ここまでくると,n入力の場合も,複雑になってきますが容易に想像がつき作成できます.まずは以下のように展開します.
![]()
次に,f(0,x2,x3)とf(1,x2,x3) をx2についてそれぞれ展開し,さらにx3について展開すると以下のようになります.
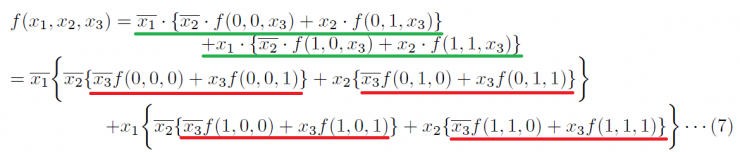
また,真理値表化も表6のようになるのは分かると思います.
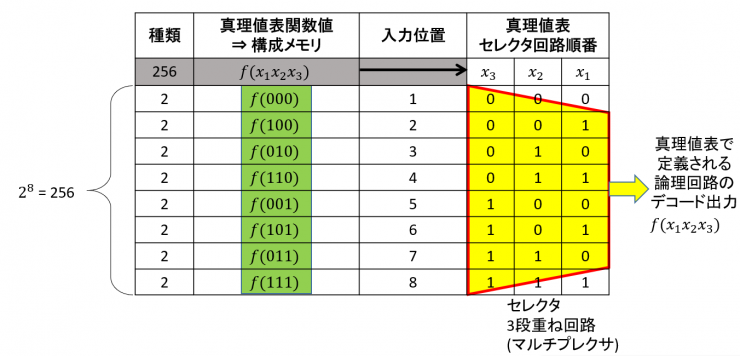
表6 式(7)を表現した真理値表
3入力の場合は2の8乗,つまり256通りのブール関数があり,表6に示す通りです.セレクタ回路が入るデコード順も,式(6)を括弧の内側からx3,x2,x1のようにたどると逆順になることも分かります.
* *
いかがでしたでしょうか.本稿を読んで,
・任意の論理関数のシャノン展開が真理値表表現になっている.
・真理値表の関数値を構成メモリに設定すれば,論理関数で展開される順序がセレクタ論理になっている.
・セレクタ回路で直接デコードできるので論理関数の出力が得られる.
という3つのポイントを押さえておいていただければと思います.
コラム1 シャノン展開理論がFPGA設計に使われる理由
●式の展開方法はシャノンが発表した論文の中にあった
計算機が発明された頃は,電磁式のリレーというスイッチング回路方式において,aとaの否定の2端子スイッチングが設計されました.通信理論(情報理論)の創始者で有名なシャノンが1938年(4)と1949年(5)にリレー式に使われるスイッチング理論の論文を発表しました.そこで議論された論理式の展開方法が,今日セレクタ論理と呼ぶ論理式で展開した式そのもので,これを「シャノン展開」と呼びます.
●シャノン展開式で真理値表を表現することができる
シャノン展開が素晴らしいのは,その展開式が真理値表そのものを表現しているからです.それでシャノン展開の理論が今日のFPGA設計において見事に復活したのです.シャノンの論文を読む時は,今日の我々の論理積と論理和の記号の意味が逆(双対という)になっています.
シャノン展開という呼び方については,電子計算機が登場してから発表したのがシャノンですが,電子計算機がない時代にブール代数(0と1の2値を扱う論理代数)でおなじみのブールが1854年にすでに考えていたために(6),ブールの展開定理と呼ぶ学者もいます(7,8,9)シャノン展開について書かれた日本語の本として,笹尾勤(10)があります.
コラム2 メーカによってルックアップ・テーブルの入力数は異なる
最近のFPGAのメーカが実際に実装している入力数は,Intel(旧Altera)社が4入力,Xilinx社が6入力です.演算器をルックアップ・テーブルを用いて設計する場合,carry chainという桁上げ伝播が発生し,しかも合計が出る前に入出力が伴い,同じルックアップ・テーブルのレベルで扱えないという問題があります.それをどのような形で吸収していくのか,メーカ各社によって考え方に違いがあります.
□参考文献□
(1)ALTERA White Paper: FPGA Architecture.
(2)Xilinx:7 Series FPGAs Configurable Logic Block, User Guide.
(3)天野英晴 編:FPGAの原理と構成,オーム社 2016;英訳版, Amano, H.: Principles and Structures of FPGAs, Springer,2018
(4)Shannon, C. E.: A Symbolic Analysis of Relay and Switching Circuits, Transactions American Institute of Electrical Engineers, vol. 57, pp. 713-723,1938
(5)Shannon, C. E.: The Synthesis of Two-Terminal Switching Circuits, Bell System Tech. J., vol. 28, no. 1, pp.59-98, 1949
(6)Boole, G.: An Investigation of the Laws of Thought, Walton and Maberly,1854
(7)Brown, F. M.: Boolean Reasoning the Logic of Boolean Equations, Springer Science+Business, LLC,1990
(8)Hachtel G. D., Somenzi F.: Logic Synthesis and Verifications Algorithms, Kluwer Academic Publishers,2002
(9)Crama, Y., Hammer, P. L.: Boolean Functions Theory, Algorithms, and Applications, Cambridge University Press,2011
(10)笹尾勤:論理設計 スイッチング回路理論 第4版,近代科学社,2005
外村 元伸